ベータ分布(beta distribution)は連続型の確率分布です。ベータ分布には第1種ベータ分布と第2種ベータ分布があり、単にベータ分布と呼ぶときには第1種ベータ分布のことを指します。ベータ分布は他の分布とたくさんの関係を持っており、パラメータの条件によっては、一様分布やベキ関数分布、ガンマ分布、カイ2乗分布などになります。
ベータ分布は、コイン投げのようにベルヌーイ試行における予測分布として使用されます。より正確には、事前分布が一様分布、尤度が2項分布のときに事後分布がベータ分布になります。
目次
ベータ分布の基本情報
※ 表は横にスクロールできます。
| パラメータ | \(0 < \alpha,\ \ \ 0 < \beta\) |
| 確率変数の範囲 | \(0\leq x \leq 1\) |
| 確率密度関数 | \(\displaystyle\frac{ x^{\alpha-1}(1-x)^{\beta-1} }{ B(\alpha,\beta) }\) ただし、\(B(\alpha,\beta)\)はベータ関数です。 \(\displaystyle B(\alpha,\beta) = \int_{0}^{1}u^{\alpha-1}(1-u)^{\beta-1}du\) |
| 累積分布関数 | \(\displaystyle I_{x}(\alpha,\beta)\) ただし、\(\displaystyle I_{x}(\alpha,\beta)\)は不完全ベータ関数比です。 不完全ベータ関数ではないので注意が必要です。 \(\displaystyle I_{x}(\alpha,\beta) = \frac{1}{B(\alpha,\beta) }\int_{0}^{x}u^{\alpha-1}(1-u)^{\beta-1}du\) |
| 積率母関数 | \(\displaystyle 1+\sum_{k=1}^{\infty}\left( \prod_{r=0}^{k-1}\frac{\alpha+r}{\alpha+\beta+r} \right)\frac{t^{k}}{k!} \) |
| 特性関数 | \(\displaystyle _{1}\!F_{1}(\alpha,\alpha+\beta;it) =1+\sum_{k=1}^{\infty}\left( \prod_{r=0}^{k-1}\frac{\alpha+r}{\alpha+\beta+r} \right)\frac{(it)^{k}}{k!}\) ただし、\(_{1}F_{1}(\alpha,\alpha+\beta;it)\)は合流型超幾何関数で次式で定義されています。 \(\displaystyle _{1}F_{1}(a,b;z)=\frac{1}{B(a,b)}\int_{0}^{1}e^{zt}t^{a-1}(1-t)^{b-a-1}dt\) |
| \(r\)次モーメント (原点まわり) |
\(\displaystyle\prod_{j=0}^{r-1}\frac{\alpha+j}{\alpha+\beta+j}=\frac{B(\alpha+r,\beta)}{B(\alpha,\beta)}=\frac{\Gamma(\alpha+r)\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\alpha+\beta+r)}\) |
| r次モーメント (平均まわり) |
\(\lambda=(\alpha+\beta)^{-1},\ \ \theta=\alpha(\alpha+\beta)^{-1}\)とおくと、\(r\)次の平均まわりの モーメント\(\mu_{r}\)に関して、次の式が成り立ちます。 \(\displaystyle \mu_{r+1} =\frac{ r\lambda }{ 1+r\lambda }\mu_{r}+\theta\sum_{j=1}^{r}\ _{r}C_{j}\frac{\lambda^{j}(1-\theta)^{j}j!}{(1+r\lambda)\cdots\{1+(r-j)\lambda\}}\mu_{r-j} \) \(\mu_{0}=1,\ \ \ \mu_{1}=0\) |
| 期待値 | \( \displaystyle\frac{\alpha}{\alpha+\beta} \) |
| 分散 | \( \displaystyle\frac{\alpha\beta}{(\alpha+\beta)^{2}(\alpha+\beta+1)} \) |
| モード | \( \displaystyle\frac{\alpha-1}{\alpha+\beta-2},\ \ \alpha > 1,\ \ \beta > 1 \) |
| 歪度 |
\(\displaystyle \frac{2(\beta-\alpha)(\alpha+\beta+1)^{\frac{1}{2}}}{(\alpha+\beta+2)(\alpha\beta)^{\frac{1}{2}}}\) |
| 尖度 | \(\displaystyle\frac{3(\alpha+\beta)(\alpha+\beta+1)(\beta+1)(2\beta-\alpha)}{\alpha\beta(\alpha+\beta+2)(\alpha+\beta+3)}+\frac{\alpha(\alpha-\beta)}{\alpha+\beta} \) |
証明一覧
確率密度関数
様々な\(\alpha,\beta\)に対応するベータ分布の確率密度関数は次のようになります。
・\(\alpha > 0,\beta >0\)のとき、\((\alpha-1)/(\alpha+\beta-2)\)で最小値をとり、関数の形は\(U\)字型になります。
・\(\alpha < 1,\beta <1\)のとき、\((\alpha-1)/(\alpha+\beta-2)\)で単一のモードをとります。
・\(\alpha =\beta\)のとき、\(1/2\)を中心に対称になります。
1.png)
\(\alpha=2\)で固定した場合の確率密度関数は次のようになります。
・\((\alpha-1)(\beta-1) \leq 0\)のとき、関数は最小値を持たず、関数の形は\(J\)字型になります。
2.png)
\(\beta=4\)で固定した場合の確率密度関数は次のようになります。
3.png)
ベータ分布を考える上での基礎知識
(1)ベータ関数
B(\alpha,\beta) = \int_{0}^{1}u^{\alpha-1}(1-u)^{\beta-1}du,\ \ \ 0\leq u\leq 1
\end{align}
(2)ガンマ関数
\Gamma(a) = \int_{0}^{\infty}\exp[-u]u^{a-1}du,\ \ \ a>0
\end{align}
(3)ディガンマ関数(プサイ関数)
\psi(a) = \frac{d}{da}\log\Gamma(a) = \frac{\displaystyle\frac{d\Gamma(a)}{da}}{\Gamma(a)}
\end{align}
ベータ関数とガンマ関数
ベータ関数とガンマ関数には次のような関係があります。
B(\alpha,\beta)=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} = B(\beta,\alpha)
\end{align}
ベータ関数の基本性質
ベータ関数は以下のような性質を持っています。
B(\alpha+1,\beta)=\frac{\alpha}{\alpha+\beta}B(\alpha,\beta)
\end{align}
特に\(\alpha,\beta\)が整数のとき、次式が成り立ちます。
B(\alpha,\beta) &= \frac{(\alpha-1)!(\beta-1)!}{(\alpha+\beta-1)!} \\
B(1,1) &= 1\\
B\left( \frac{1}{2},\frac{1}{2} \right) &= \pi
\end{align}
ガンマ関数の基本性質
ガンマ関数は以下のような性質を持っています。
\Gamma(a)=(a-1)\Gamma(a-1)
\end{align}
特に\(a\)が整数のとき、次式が成り立ちます。
\Gamma(a) &= (a-1)! \\
\Gamma(0) &= 1 \\
\Gamma(1) &= 1 \\
\Gamma\left( \frac{1}{2} \right) &= \sqrt{\pi} \\
\Gamma\left( a+\frac{1}{2} \right) &= \frac{(2a)!\sqrt{\pi}}{a!2^{2a}}
\end{align}
ベータ分布族
ベータ分布族の確率密度関数は次式で与えられます。
\frac{1}{B(\alpha,\beta)}\frac{(y-a)^{\alpha-1}(b-y)^{\beta-1}}{(b-a)^{\alpha+\beta-1}},\ \ \ a\leq y \leq b,\ \ \alpha >0,\ \ \beta >0
\end{align}
とくに、\(\beta=1\)のときベキ関数分布と呼ばれます。
変数\(X\)を
X=\frac{Y-1}{b-a}
\end{align}
で置き換えると、\(X\)の確率密度関数はベータ分布の標準形
\frac{ x^{\alpha-1}(1-x)^{\beta-1} }{ B(\alpha,\beta) }
\end{align}
となります。
ベータ分布と他の分布との関係
一様分布
ベータ分布に従う確率変数\(X\sim Beta(1,1)\)は一様分布に従います。
ベキ関数分布
ベータ分布に従う確率変数\(X\sim Beta(1,\beta)\)はベキ関数分布に従います。
2項分布
ベータ分布に従う確率変数\(X\sim Beta(i,n-1+1)\)(\(n,i\)は正の整数)と、パラメータ\(n,p\)の2項分布に従う確率変数\(Y\sim Bin(n,p)\)には次のような関係があります。
\mathrm{P}(X\leq p) = \mathrm{P}(Y\geq i)
\end{align}
\(F\)分布
ベータ分布に従う確率変数\(X\sim Beta(\frac{\alpha}{2},\frac{\beta}{2})\)と、\(F\)分布に従う確率変数\(Y\sim F(\beta,\alpha)\)には次のような関係があります。
\mathrm{P}\left( X\leq \frac{\alpha}{\alpha+\beta x} \right)=\mathrm{P}(Y > x)
\end{align}
ガンマ分布
パラメータ\(p,q\)を用いたガンマ分布に従う確率変数は、任意のパラメータ\(\alpha >0\)を用いたベータ分布と次のような関係があります。
Beta(p,q) &= \frac{ Gam(p,\alpha) }{ Gam(p,\alpha)+Gam(q,\alpha) }
\end{align}
カイ2乗分布
確率変数\(X_{1},X_{2}\)を互いに独立に、自由度\(m_{1},m_{2}\)のカイ2乗分布に従う確率変数とすると、以下のようなことが成り立ちます。
\frac{X_{1}}{X_{1}+X_{2}}\sim Beta\left( \frac{m_{1}}{2},\frac{m_{2}}{2} \right)
\end{align}
標準正規分布
\(\frac{\alpha}{\beta}\)を一定に保ちながら、\(\alpha\rightarrow\infty\),\(\beta\rightarrow\infty\)となるとき、\(Beta(\alpha,\beta)\)は標準正規分布\(N(0,1)\)に収束します。
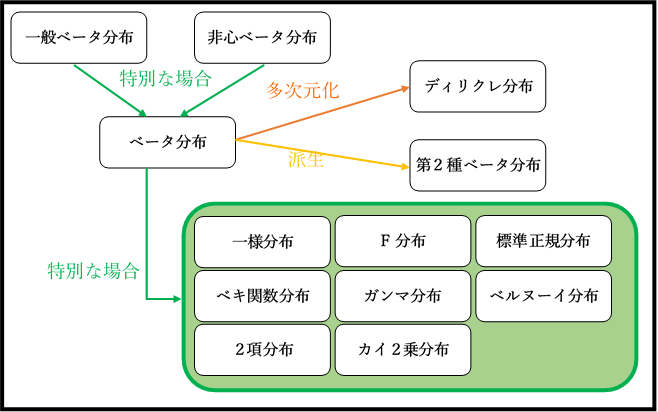
ベータ分布と関連深い他の分布との関係
ベータ分布と関係の深いところにある、分布をまとめました。イメージ作りにどうぞ。
各分布については下のリンクからお願いします。
2-100x100.png)
3-100x100.png)
-100x100.png)
-100x100.png)
