学習レベル:大学生 難易度:★☆☆☆☆
確率分布の特徴付けとして期待値、分散はよく使用される指標ですが、2つに加えて歪度・尖度が使用されることがあります。歪度・尖度の計算にはモーメント(またはキュムラント)の知識が必要になるので、モーメントが分からない方は<モーメントとはの記事>を予め参照してください。
尖度の定義
尖度(kurtosis)
確率分布の裾の長さを表す指標として尖度というものがあり、記号\(\beta_{2}\)で表し下のように定義されます。$$\beta_{2} = \frac{\mu_{4}}{\sigma^{4}}=\frac{\mu_{4}}{\mu_{2}\,^{2}}$$ここで、\(X\)を確率変数とし\(\mu\)を期待値、\(\sigma^{2}\)を分散とすると、\((X-\mu)/\sigma\)の4次モーメントが尖度となります。
※ \(\mu_{j}\)は\(j\)次の中心モーメントを表します。
尖度の見方は次のようになります。
- \(\beta_{2}\)が小さくなればなるほど、確率密度が0に近づくスピードが速くなります。
- 逆に\(\beta_{2}\)が大きくなればなるほど、確率密度が0に近づくスピードが遅くなります。
実際に、\(\beta_{2}\)の値の違いによって確率密度がどのようになるか確認してみましょう(今回の例は正規分布で行っています)。
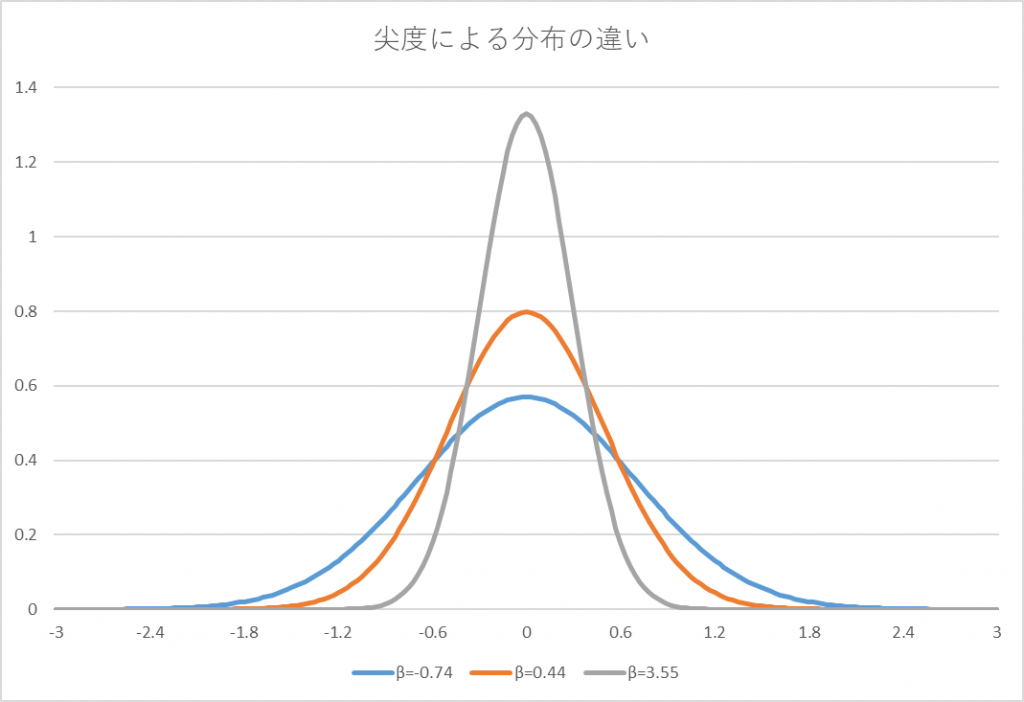
上の図から尖度が大きくなればなるほど、確率密度が0になるスピードが速いことが分かります。期待値、分散と比べると計算が大変ですが、その分得られる情報は大きいので求める価値があります。しかし、実際にグラフを描いてみるとわかってしまう情報でもあるので、あまり利用されないことも事実です。
合わせて読みたい記事
・歪度:確率分布の対称性を表します。尖度と合わせて使用されます。
・モーメント:モーメントについて定義しています。