第2種ベータ分布(反転ベータ分布、beta prime distribution、beta distribution of the second kind)は、連続型の確率分布です。確率変数\(X\)が(第1種)ベータ分布に従うとき\(\displaystyle\frac{X}{1-X}\)が従う分布が第2種ベータ分布です。第2種ベータ分布に従う確率変数\(X\)は、記号\(Beta^{\prime}\)を用いて、\(X\sim Beta^{\prime}(\alpha,\beta)\)と表されます。
第2種ベータ分布はあまりお目にかかることはないですが、計算上知っておくと便利なこともあるので、雑学程度に覚えておきましょう。
第2種ベータ分布の基本情報
※ 表は横にスクロールできます。
| パラメータ | \(0 < \alpha,\ \ \ 0 < \beta\) |
| 確率変数の範囲 | \(0\leq x \) |
| 確率密度関数 | \(\displaystyle\frac{ x^{\alpha-1}(1+x)^{-\alpha-\beta} }{ B(\alpha,\beta) }\) ただし、\(B(\alpha,\beta)\)はベータ関数です。 \(\displaystyle B(\alpha,\beta) = \int_{0}^{1}u^{\alpha-1}(1-u)^{\beta-1}du\) |
| 累積分布関数 | \(\displaystyle I_{\frac{x}{1+x}}(\alpha,\beta)\) ただし、\(\displaystyle I_{x}(\alpha,\beta)\)は不完全ベータ関数比です。 不完全ベータ関数ではないので注意が必要です。 \(\displaystyle I_{x}(\alpha,\beta) = \frac{1}{B(\alpha,\beta) }\int_{0}^{x}u^{\alpha-1}(1-u)^{\beta-1}du\) |
| 積率母関数 | \(\displaystyle \frac{e^{-t}\Gamma(\alpha+\beta)}{\Gamma(\beta)}G_{1,2}^{\ 2,0}\left( \begin{array}{c|c} \alpha+\beta & \\ \beta,0 & -t \end{array}\right)\) |
| \(r\)次の原点まわりのモーメント | \(\displaystyle \prod_{k=1}^{r}\frac{\alpha+k-1}{\beta-k}\) |
| 期待値 | \( \displaystyle\frac{\alpha}{\beta-1}\ \ \ (ただし\beta>1) \) |
| 分散 | \( \displaystyle\frac{\alpha(\alpha+\beta-1)}{ (\beta-2)(\beta-1)^{2} }\ \ \ (ただし\beta>2) \) |
| モード | \( \displaystyle\frac{ \alpha-1 }{ \beta+1 }\ \ \ (ただし\alpha\geq 1で、それ以外は0) \) |
| 歪度 |
\(\displaystyle \frac{2(2\alpha+\beta-1)}{\beta-3}\sqrt{ \frac{\beta-2}{\alpha(\alpha+\beta-1)} }\ \ \ (ただし\beta>3)\) |
ただし、\(\displaystyle G_{1,2}^{\ 2,0}\left(
\begin{array}{c|c}
\alpha+\beta & \\
\beta,0 & -t
\end{array}\right)\)はMeijerのG関数であり
G_{p,q}^{\ m,n}\left(
\begin{array}{c|c}
a_{1},\cdots,a_{p} & \\
b_{1},\cdots,b_{q} & z
\end{array}\right) &= \frac{1}{2\pi i}\int_{L}\frac{ \prod_{j=1}^{m}\Gamma(b_{j}-s)\prod_{j=1}^{n}\Gamma(1-a_{j}+s) }{ \prod_{j=m+1}^{q}\Gamma(1-b_{j}+s)\prod_{j=n+1}^{p}\Gamma(a_{j}-s) }z^{s}ds
\end{align}
を表します。
証明一覧
確率密度関数
様々な\(\alpha,\beta\)に対応する第2種ベータ分布の確率密度関数は次のようになります。

一般化第2種ベータ分布
第2種ベータ分布のパラメータにさらに、実数\(p,q>0\)のパラメータを追加した次式の確率密度関数を、一般化第2種ベータ分布(generalized beta prime distribution)といいます。
f(x|\alpha,\beta,p,q) &= \frac{ p\left( \frac{x}{q} \right)^{\alpha p-1}\left( 1+\left( \frac{x}{q} \right)^{p} \right)^{-\alpha-\beta} }{ qB(\alpha,\beta) }
\end{align}
パラメータ\(p=q=1\)のとき、第2種ベータ分布\(Beta^{\prime}(\alpha,\beta)\)に従います。
第2種ベータ分布の基本性質
第2種ベータ分布が持つ特徴をまとめています。機会があれば証明もしていきたいと思います。
- 確率変数\(X\)が第2種ベータ分布\(X\sim Beta^{\prime}(\alpha,\beta)\)に従うとき、逆数も第2種ベータ分布\(X\sim Beta^{\prime}(\beta,\alpha)\)に従います。
- 確率変数\(X\)が一般化第2種ベータ分布\(X\sim Beta^{\prime}(\alpha,\beta,p,q)\)に従うとき、スカラー倍した確率変数も一般化第2種ベータ分布\(kX\sim Beta^{\prime}(\alpha,\beta,p,kq)\)に従います。
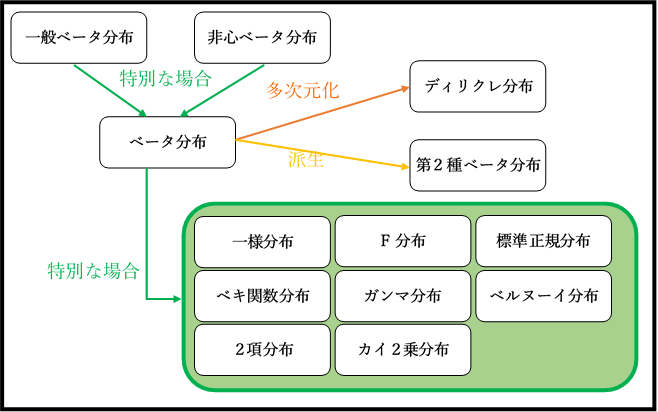
第2種ベータ分布と他の分布との関係
第2種ベータ分布と他の分布との関係をまとめています。
- 確率変数\(X\)が\(F\)分布\(X\sim F(2\alpha,2\beta)\)に従うとき、このとき\begin{align}\frac{\alpha}{\beta}X\sim Beta^{\prime}(\alpha,\beta)もしくはX\sim Beta^{\prime}(\alpha,\beta,1,\frac{\beta}{\alpha})\end{align}となります。
- 確率変数\(X\)がベータ分布\(X\sim Beta(\alpha,\beta)\)に従うとき、\(X/(1-X)\)は第2種ベータ分布\begin{align}\frac{X}{1-X}\sim Beta^{\prime}(\alpha,\beta)\end{align}に従います。
- 確率変数\(X,Y\)が互いに独立にガンマ分布\(X\sim Gam(\alpha,1),\ Y\sim Gam(\beta,1)\)に従っているとき、\begin{align}\frac{X}{Y}\sim Beta^{\prime}(\alpha,\beta)\end{align}が成り立ちます。
- 第2種ベータ分布のパラメータが\(\beta=1\)のとき、確率変数\(X\sim Beta^{\prime}(\alpha,1,p,q)\)は、Dagum分布\(Dagum(\alpha,p,q)\)と同等になります。
- 第2種ベータ分布のパラメータが\(\alpha=1\)のとき、確率変数\(X\sim Beta^{\prime}(1,\beta,p,q)\)は、Burr分布\(SinghMaddala(\beta,p,q)\)と同等になります。
- 第2種ベータ分布のパラメータが\(\alpha=\beta=1\)のとき、確率変数\(X\sim Beta^{\prime}(1,1,p,q)\)は、対数ロジスティクス分布\(LL(p,q)\)と同等になります。
第2種ベータ分布と関連深い他の分布との関係
第2種ベータ分布と関係の深いところにある、分布をまとめました。イメージ作りにどうぞ。
各分布については下のリンクからお願いします。

1-100x100.png)
