ディリクレ分布(Dirichlet distribution)は連続型の確率分布で、ベータ分布を多次元化したものになります。
ディリクレ分布は、同時に発生することがない\(k\)個の事象\(A_{1},\cdots,A_{k}\)において、それぞれの事象が\(\alpha_{i}-1\)回発生することを考えます。このとき、事象\(A_{i}\)が起こる確率\(x_{i}\)がディリクレ分布に従います。
この分布はカイ2乗分布から作成することができ、\(Y_{0},Y_{1},\cdots,Y_{k}\)が互いに独立に自由度\(m_{0},m_{1},\cdots,m_{k}\)のカイ2乗分布に従うとします。このとき\(m_{i}\)は整数でなければならないが、必ずしも整数でなくても構いません。このとき
X_{j} &= \frac{Y_{j}}{\displaystyle\sum_{i=0}^{k}Y_{i}},\ \ \ \ j=1,\cdots,k
\end{align}
とすると、\(X_{1},\cdots,X_{k}\)の同時確率密度関数はパラメータ\(\alpha_{i}=m_{i}/2\)のディリクレ分布に従います。
ディリクレ分布に従う確率変数は、記号\(Dir\)を用いて\(X\sim Dir(\alpha)\)と表されます。
目次
ディリクレ分布の基本情報
※ 表は横にスクロールできます。
| パラメータ | \(\alpha_{i} > 0,\ \ \ i=1,\cdots,k\) |
| 確率変数の範囲 | \( x_{i}\geq0,\ \ \ \ \displaystyle\sum_{i=1}^{k}x_{i}\leq 1 \) |
| 確率密度関数 | \(\displaystyle \frac{1}{B(\alpha)}\prod_{i=1}^{k}x_{i}^{\alpha_{i}-1} \) ただし、\(\alpha=(\alpha_{1},\cdots,\alpha_{k})\),\(B(\alpha)\)は多変量ベータ関数です。 \(\displaystyle B(\alpha) =\frac{\prod_{i=1}^{k}\Gamma(\alpha_{i})}{\Gamma\left( \sum_{i=1}^{k}\alpha_{i} \right)}\) |
| 累積分布関数 | なし |
| 期待値 | \( \displaystyle\frac{\alpha_{i}}{\alpha_{0}} \) ただし、\(\alpha_{0}=\sum_{i=1}^{n}\alpha_{i}\)です。 |
| 分散 | \( \displaystyle\frac{ \alpha_{i}(\alpha_{0}-\alpha_{i}) }{ \alpha_{0}^{2}(\alpha_{0}+1) } \) |
| 共分散 | \( \displaystyle\frac{-\alpha_{i}\alpha_{j}}{\alpha_{0}^{2}(\alpha+1)},\ \ \ \ i\neq j \) |
| モード | \( \displaystyle\frac{\alpha_{i}-1}{\alpha_{0}-k} \) |
証明一覧
ディリクレ分布を考える上での基礎知識
(1)ベータ関数
B(\alpha,\beta) = \int_{0}^{1}u^{\alpha-1}(1-u)^{\beta-1}du,\ \ \ 0\leq u\leq 1
\end{align}
(2)ガンマ関数
\Gamma(a) = \int_{0}^{\infty}\exp[-u]u^{a-1}du,\ \ \ a>0
\end{align}
(3)ディガンマ関数(プサイ関数)
\psi(a) = \frac{d}{da}\log\Gamma(a) = \frac{\displaystyle\frac{d\Gamma(a)}{da}}{\Gamma(a)}
\end{align}
ベータ関数とガンマ関数
ベータ関数とガンマ関数には次のような関係があります。
B(\alpha,\beta)=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} = B(\beta,\alpha)
\end{align}
ベータ関数の基本性質
ベータ関数は以下のような性質を持っています。
B(\alpha+1,\beta)=\frac{\alpha}{\alpha+\beta}B(\alpha,\beta)
\end{align}
特に\(\alpha,\beta\)が整数のとき、次式が成り立ちます。
B(\alpha,\beta) &= \frac{(\alpha-1)!(\beta-1)!}{(\alpha+\beta-1)!} \\
B(1,1) &= 1\\
B\left( \frac{1}{2},\frac{1}{2} \right) &= \pi
\end{align}
ガンマ関数の基本性質
ガンマ関数は以下のような性質を持っています。
\Gamma(a)=(a-1)\Gamma(a-1)
\end{align}
特に\(a\)が整数のとき、次式が成り立ちます。
\Gamma(a) &= (a-1)! \\
\Gamma(0) &= 1 \\
\Gamma(1) &= 1 \\
\Gamma\left( \frac{1}{2} \right) &= \sqrt{\pi} \\
\Gamma\left( a+\frac{1}{2} \right) &= \frac{(2a)!\sqrt{\pi}}{a!2^{2a}}
\end{align}
ディリクレ分布とベータ分布
ディリクレ分布に従う確率変数\(X\sim Dir(\alpha)\)について\(k=1\)としたとき、\(X\)はパラメータ\(\alpha=\alpha_{1},\ \ \beta=m_{0}/2\)のベータ分布に従います。このことから、ディリクレ分布はベータ分布を拡張したものだと確認することができます。
ディリクレ分布と標準ガンマ分布
ディリクレ分布に従う確率変数\(X=(X_{1},\cdots,X_{k})\sim Dir(\alpha)\)について、\(X\)の要素\(X_{j}\)は、\(Y_{i}\)を標準ガンマ分布に従う確率変数\(Y_{i}\sim Gam(\alpha_{i},1)\)とすると、次の関係があります。
X_{j} = \frac{Y_{j}}{\sum_{i=0}^{k}Y_{i}},\ \ \ \ j=1,\cdots,k
\end{align}
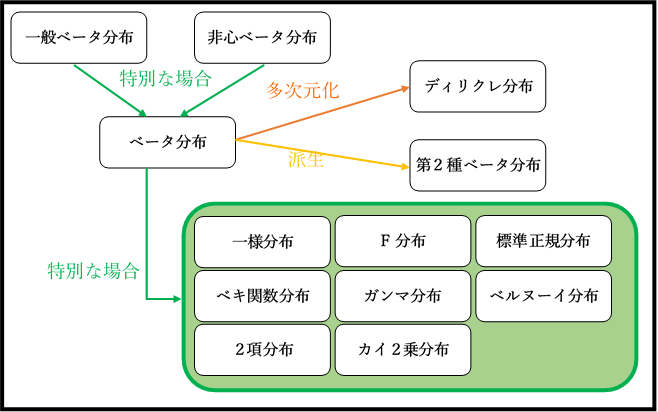
ディリクレ分布と関連深い他の分布との関係
ディリクレ分布と関係の深いところにある、分布をまとめました。イメージ作りにどうぞ。
各分布については下のリンクからお願いします。

1-100x100.png)