中央値とは

学習レベル：中学生　難易度：★☆☆☆☆

代表値(averages)とは、データの分布を特徴づけるための数字です。中央値も特徴付けを行う、数字のひとつであり中央値に関する研究もかなり行われているので、この記事を読んで是非マスターしていきましょう！

1 中央値とは
- 1.1 具体例１（データ数が奇数の場合）
- 1.2 具体例２（データ数が偶数の場合）
2 中央値の性質
3 中央値のまとめ
4 その他の平均

　データの分布が左右対称に近いデータでしたら、算術平均、刈り込み平均を用いればいいのですが、左右対称からかなり離れたデータに対して、これら平均を用いると全く意味を持たないものになってしまいます。次の表を見てみましょう！

	A	B	C	D	E	F	G	H	I
点数	1	1	1	1	1	1	2	3	10

このデータに算術平均$x_{a}$をとり、ヒストグラムを描いてみると次のようになります。

$$x_{a} = \frac{1}{9}\left( 1+1+\cdots+10 \right)\approx2.33$$

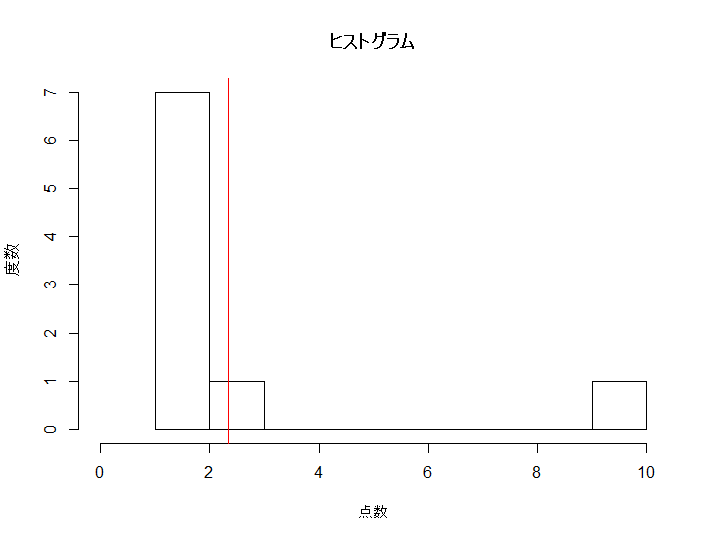
ヒストグラムに引いてある赤線は算術平均を表します。

ほとんどのデータが赤線の左側にあって、
右側にはほとんどデータがないですね

そうなんです。
このデータに算術平均を用いても、平均の役割を果たさないですよね？
このように偏りのあるデータに対して中央値を用います。

中央値(メディアン median)

データ数$n$のデータ$ X_{1},X_{2},\cdots,X_{n} $が得られたとき中央値$x_{me}$は以下のように定義されます。

１：データを小さいものから順番に並べます。並び替えたものを改めて次のようにおきます。$$X_{1}^{\ast},X_{2}^{\ast},\cdots,X_{n}^{\ast}$$ ２：このデータに対して中央値$x_{me}$は次のようになります。

\begin{align} x_{me}=\left\{\begin{array}{cc} &X_{\frac{n+1}{2}}^{\ast}\ \ \mbox{（$n$が奇数の場合）} \\ &\frac{1}{2}\left( X_{\frac{n}{2}}^{\ast}+X_{\frac{n}{2}+1}^{\ast} \right)\ \ \mbox{（$n$が偶数の場合）} \end{array}\right. \end{align}

数式だと難しそうですが、中央値はデータを小さい順に並び替えたとき、ちょうど真ん中にくるデータのことです。
具体例を２つ見てみましょう！

具体例１（データ数が奇数の場合）

データ数が奇数だった場合、データの中心は分かりやすいです。
次の表データの中央値を求めてみましょう！

	A	B	C	D	E	F	G	H	I
点数	1	1	1	1	1	1	2	3	10

まずデータを小さい順に並べます！

\begin{align}X_{1}^{\ast}=1,\ X_{2}^{\ast}=1,\cdots,X_{9}^{\ast}=10\end{align}

データ数が9個なので中央値となるデータ番号は$$\frac{9+1}{2}=5$$より5番目のデータを選べばよい。よって中央値$x_{me}$は、$$x_{me}=X_{5}^{\ast}=1$$となります。

具体例２（データ数が偶数の場合）

データ数が偶数のとき、ちょうど中心になるデータがありません。このようなとき、中央値をどのように求めるか具体例を見てみましょう！

	A	B	C	D	E	F
点数	9	2	4	2	6	6

先ほどと同様にデータを小さい順に並び替えます！

\begin{align}X_{1}^{\ast}=2,\ X_{2}^{\ast}=2,\ X_{3}^{\ast}=4,\ X_{4}^{\ast}=6,\ X_{5}^{\ast}=6,\ X_{6}^{\ast}=9\end{align}

データ数が6なので偶数である。このとき、中央値を求める際に用いるデータ番号は$$\frac{6}{2}=3,\ \ \ \ \ \frac{6}{2}+1=4$$となります（つまり、データの中心の前後のデータを用いるということになります）。このとき中央値$x_{me}$は、$$x_{me}=\frac{X_{3}^{\ast}+X_{4}^{\ast}}{2}=\frac{4+6}{2}=5$$となります。

中央値の弱点ってありますか？

データ数が非常に大きくなったとき、データを小さい順に並べる手間が非常に大きくなります。手計算で中央値を求める際にも思いますよね？
これはコンピュータで計算させるときも同じことなんです！

中央値の性質

少し難しい話になるのですが、中央値を学ぶ上でとっても大切な性質になります。中央値は平均偏差を最小化する性質をもっています。数学的に中央値は$$T(t)=\sum_{i=1}^{n}\left| x_{i}-t \right|$$を最小化する$ t $で定義されています。$T(t) $をデータ数$ n $で割ったもの$$\frac{1}{n}\sum_{i=1}^{n}\left| x_{i}-t \right|$$を平均偏差といいます。

※　平均偏差の詳細は＜平均偏差の記事＞で説明しています。

中央値のまとめ

中央値はデータの分布が左右対称でないものに対して、力を発揮する平均のひとつです。データ数が奇数のときと、偶数のときで中央値の求め方が変わるので注意してください。中央値は、平方偏差を最小化する重要な性質を持っています。現時点で覚えるのは難しいですが、知識として蓄えておきましょう！

その他の平均

・　算術平均：様々な性質をもつ、最もポピュラーな平均です。

・　刈り込み平均：異常値に対応するための算術平均のようなものです。

・　幾何平均：成長率などに用いる平均です。

・　調和平均：比に関する平均です。

・　最頻値（モード）：データをカテゴリや階級別に分けたときに用いる平均です。

中央値とは【データの中心を捉える】