学習レベル:中学生 難易度:★☆☆☆☆
経済、経営などで得られるデータのまとめ方の一つにローレンツ曲線(Lorenz curve)というものがあります。このデータのまとめ方は、所得などの格差の大きさを表すために使用されます。また、図で表すだけではなく、ジニ係数(Gini's coefficient)と呼ばれる具体的な数字で比較する方法も紹介します。この記事では具体例も交えてまとめていきます!
ローレンツ曲線とは
ローレンツ曲線は経済の分野などでよく使われており、データの格差を表すのに特化したデータの整理法になります。
具体的にローレンツ曲線ってどのようなものなのですか?
言葉だけだと分かりにくいので具体例を見てみましょう!
| A | B | C | D | E | 計 | ||
| 会社1 | 給与金額(万円) | 200 | 200 | 200 | 200 | 200 | 1000 |
| 相対度数 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 1.0 | |
| 累積相対度数 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | ||
| 会社2 | 給与金額(万円) | 100 | 100 | 200 | 300 | 300 | 1000 |
| 相対度数 | 0.1 | 0.1 | 0.2 | 0.3 | 0.3 | 1.0 | |
| 累積相対度数 | 0.1 | 0.2 | 0.4 | 0.7 | 1.0 | ||
| 会社3 | 給与金額(万円) | 0 | 0 | 100 | 100 | 300 | 500 |
| 相対度数 | 0.0 | 0.0 | 0.2 | 0.2 | 0.6 | 1.0 | |
| 累積相対度数 | 0.0 | 0.0 | 0.2 | 0.4 | 1.0 |
”統計検定2級対応 統計学基礎(日本統計学会編)より”
上の表は5人の従業員数がいる3社の給料をまとめたものである。
ローレンツ曲線はまずデータを小さい順に並べます。そして、
横軸に従業員数の累積相対度数をとり、縦軸に給与の累積相対度数をとります。
上の表を参考にローレンツ曲線を描いてみると下のようになります。
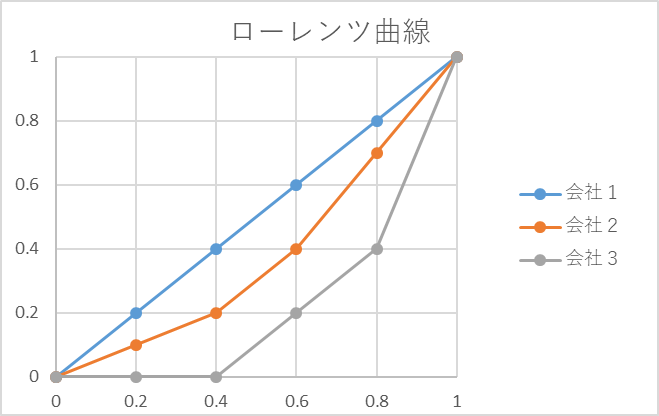
この例では会社1が完全な平等になっています。
完全な平等のとき、ローレンツ曲線は上図の青色のグラフのように直線になります。この直線を完全平等線(均等分布戦, complete equality line)と言います。
逆に不平等なほど、完全平等線からほど遠くなります。
この例では会社3が一番不平等ですね!
そうなんです!
このように図から不平等さを測ることができるのですが、具体的な数字でも不平等さを表現することができます。
ジニ係数
ローレンツ曲線は不平等さを表現する図であったが、具体的な数字で表現したものをジニ係数(Gini's coefficient)と言います。ジニ係数は完全平等線と囲まれた面積の2倍で定義されます(一番不平等だったときを1にするため2倍にします。)。
つまり、平等であればあるほど0に近くなり
不平等であればあるほど1に近くなるということですね♪
正解です!
ローレンツ曲線を描く際は、ジニ係数も一緒につけると、とても親切な図になると思います。
ローレンツ曲線のまとめ
ローレンツ曲線は、データを小さい順に並べ、横軸にデータ数の累積相対度数、縦軸にデータの累積相対度数をとることで、作成されます。完全平等のときローレンツ曲線は直線になり、不平等になればなるほど完全平等線から離れた曲線になります。
データの不平等さを表現する方法は図を用いるだけでなく、ローレンツ曲線を用いて求められるジニ係数がある。ジニ係数は完全平等なとき0をとり、不平等になればなるほど1に近くなります。