学習レベル:高校生 難易度:★★☆☆☆
2変数データを対等のものではなく、片方のデータから、もう一つの方のデータの関係や予測を行うために、使用する方法として回帰直線があります。例えば温度と湿度のデータのとき、「温度から湿度が予測できるかどうか」などに用います。
回帰直線とは
<散布図とクロス表の記事>で散布図の作成方法をまとめていました。散布図をまとめ方がわからない場合はあらかじめ復習をお願いします。
温度のデータ\(x\)と湿度のデータ\(y\)の2変数データについて考えるとき、散布図が下のようになりました。
.png)
回帰直線では温度のデータ\(x\)から湿度のデータ\(y\)を説明したり予測したりしようとする方法です。
このとき説明する方の変数\(x\)を説明変数(独立変数、予測変数など explanatory variable, independent variable)とよび、
説明される方の変数\(y\)を応答変数(目的変数、従属変数、被説明変数など response variable, dependent variable, explained variable)
といいます。
このとき回帰直線は次のように定義されます。
回帰係数の推定方法
回帰係数の推定には最小二乗法を用います。
最小二乗法を定義する前に残差について定義します。
この残差を用いて、回帰係数を推定していきます。
統計学でよく使われる最小二乗法を紹介します。
実は回帰係数の最小二乗法による推定量は次の式で求まります。
どうですか?
回帰係数の最小二乗推定量を求めるだけなら簡単ですよね?
しかし、なぜこの式で求められるか知りたい方は下のほうの証明をご覧ください。
上の温度と湿度について、回帰直線を引いてみると次のようになります。
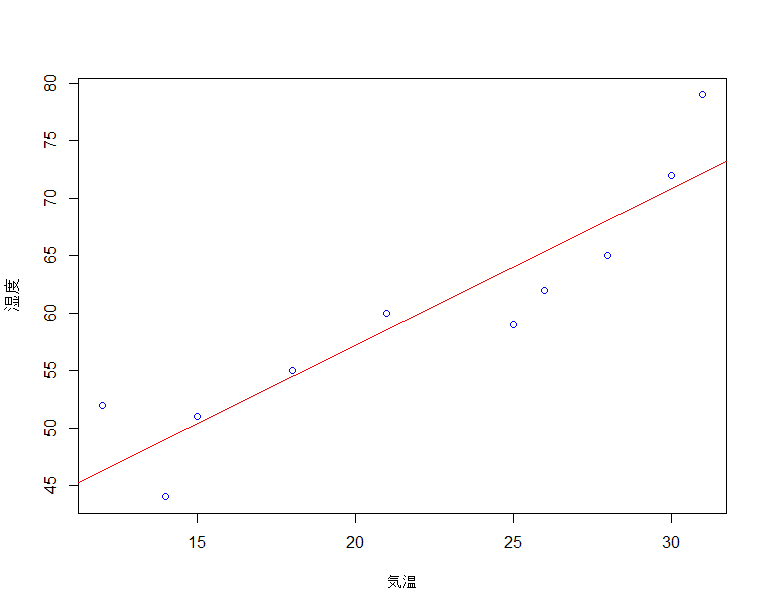
散布図で相関関係を見るよりも、より分かりやすく相関関係が見れると思います。この回帰直線では、説明変数が1種類でしたが、実は複数個の説明変数を用いる重回帰分析というものがあります。
回帰係数の最小二乗推定量の証明
■証明
残差平方和の式を見てみると$$S(\widehat{\alpha},\widehat{\beta}) = \sum_{i=1}^{n}\{ y_{i}-(\widehat{\alpha}+\widehat{\beta}x_{i}) \}^{2}$$となります。\(\widehat{\alpha}、\widehat{\beta}\)にそれぞれ注目すると少なくとも下に凸の放物線になることが分かります。よって、\(\widehat{\alpha}、\widehat{\beta}\)それぞれで微分した式がイコール0になるように\(\widehat{\alpha}、\widehat{\beta}\)を計算するといいことがわかります。それぞれで微分してイコール0とすると
n\widehat{\alpha}+\widehat{\beta}\sum_{i=1}^{n}x_{i}-\sum_{i=1}^{n}y_{i} &= 0\\
\widehat{\alpha}\sum_{i=1}^{n}x_{i}+\widehat{\beta}\sum_{i=1}^{n}x_{i}^{2}-\sum_{i=1}^{n}x_{i}y_{i} &= 0
\end{align}
という連立方程式がたてられます。この式を正規方程式といいます。この連立方程式を解くと、求めたい結果が得られます。
□
回帰直線のまとめ
回帰直線は2変数データに対して、片方のデータから、もう一つの方のデータの関係や予測を行う方法です。回帰直線において興味があるのは回帰係数の推定です。回帰係数は最小二乗法を用いて推定します。この結果は公式化されているので、比較的計算しやすいというのもひとつの特徴です。